Como vimos no cap. 9, a radiação eletromagnética de quadrupolo elétrico no limite de grandes comprimentos de onda pode ser bastante complicada. De maneira geral, ela é caracterizada pelo tensor de quadrupolo (em geral complexo) dado por:
Qij = ∫(3xiyj-δijr2)ρ(x)d3x,
onde a densidade de carga oscila harmonicamente, dada por ρ(x,t)=Re[e-iωtρ(x)] onde ρ(x) é, em geral, complexo. O tensor de quadrupolo elétrico é um tensor simétrico de traço nulo. No caso particular em que ele é real, sempre existe um sistema de eixos ortogonais no qual ele é diagonal (os eixos representam os auto-vetores do tensor). Nesse sistema de eixos particular, seus elementos diagonais podem ser escritos de maneira geral como Q11=a, Q22=b e Q33=-a-b, com a e b reais quaisquer. Podemos parametrizá-los como a=Q cos ψ e b= Q sin ψ. A distribuição angular de potência irradiada é proporcional a [Jackson, Eq. (9.45)]:
f(θ,φ) = |[nxQ]xn|2=|Q⋅n|2-|n⋅Q⋅n|2
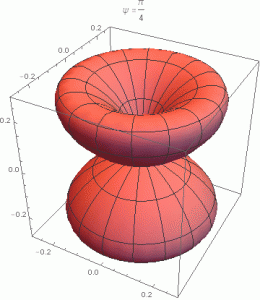
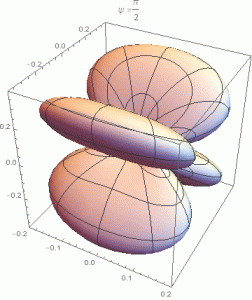
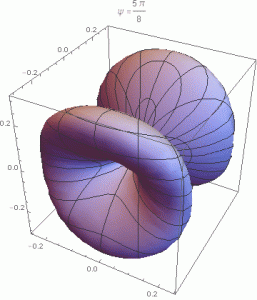
onde n=sinθ(cosφx+sinφy)+cosθz e θ e φ são os ângulos esféricos. É evidente que a constante Q não afeta a distribuição angular, que depende apenas de ψ, que, por sua vez, varia de 0 a 2π (na verdade, a distribuição angular é periódica em ψ com período π). As imagens abaixo mostram a distribuição angular acima (num gráfico 3D), para vários valores de ψ no seu intervalo de variação. A Figura 9.2 do livro do Jackson corresponde ao caso ψ=π/4.
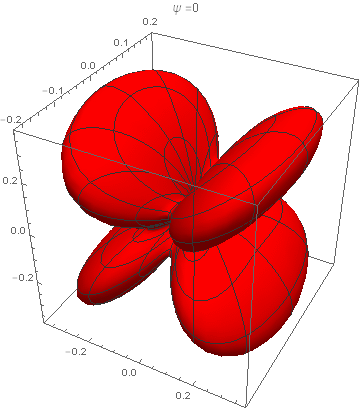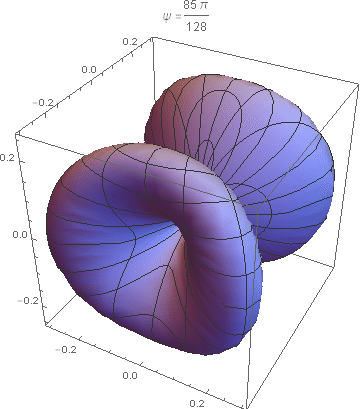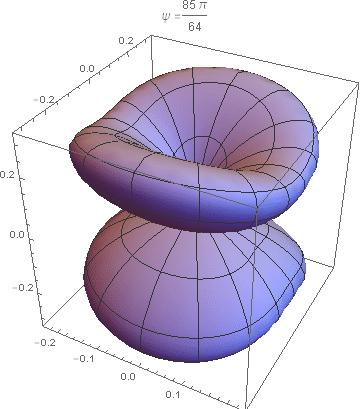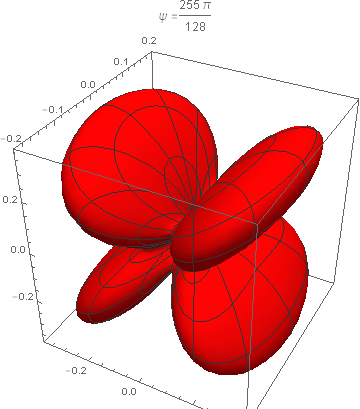
(Imagens geradas por Guilherme Fórnias Machado de Rezende)