http://scholar.google.com/citations?hl=en&user=95SvbM8AAAAJ
1.
Moreira, DA; Albuquerque, EL; da Silva, LR; Galvao, DS
Low-temperature specific heat spectra considering nonextensive long-range correlated quasiperiodic DNA molecules Journal Article
Em: Physica A: Statistical Mechanics and its Applications, vol. 387, não 22, pp. 5477–5482, 2008.
@article{moreira2008low,
title = {Low-temperature specific heat spectra considering nonextensive long-range correlated quasiperiodic DNA molecules},
author = {Moreira, DA and Albuquerque, EL and da Silva, LR and Galvao, DS},
url = {http://www.sciencedirect.com/science/article/pii/S0378437108005347},
year = {2008},
date = {2008-01-01},
journal = {Physica A: Statistical Mechanics and its Applications},
volume = {387},
number = {22},
pages = {5477--5482},
publisher = {North-Holland},
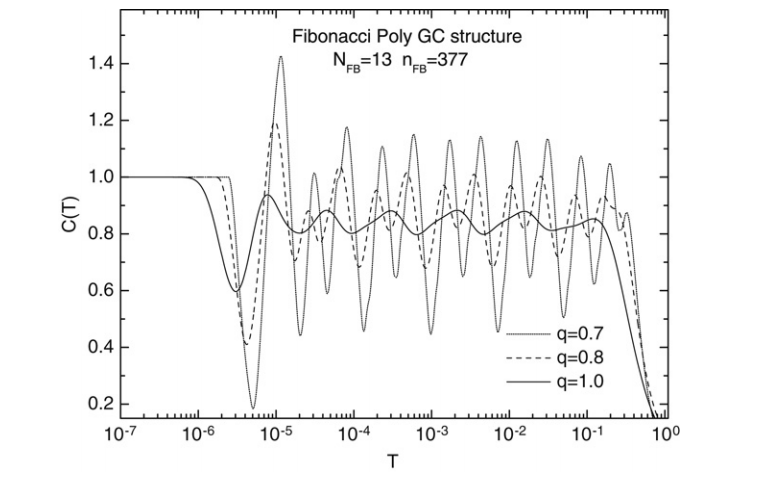
abstract = {We consider the low-temperature specific heat spectra of long-range correlated quasiperiodic DNA molecules using a q-gaussian distribution, and compare them with those considering the Boltzmann-Gibbs distribution. The energy spectra are calculated using the one-dimensional Schrödinger equation in a tight-binding approximation with the on-site energy exhibiting long-range disorder and non-random hopping amplitudes. We focus our attention at the low temperature region, where the specific heat spectra presents a logarithmic-periodic oscillations as a function of the temperature T around a mean value given by a characteristic dimension of the energy spectrum.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
We consider the low-temperature specific heat spectra of long-range correlated quasiperiodic DNA molecules using a q-gaussian distribution, and compare them with those considering the Boltzmann-Gibbs distribution. The energy spectra are calculated using the one-dimensional Schrödinger equation in a tight-binding approximation with the on-site energy exhibiting long-range disorder and non-random hopping amplitudes. We focus our attention at the low temperature region, where the specific heat spectra presents a logarithmic-periodic oscillations as a function of the temperature T around a mean value given by a characteristic dimension of the energy spectrum.
2008
1.
Moreira, DA; Albuquerque, EL; da Silva, LR; Galvao, DS
Low-temperature specific heat spectra considering nonextensive long-range correlated quasiperiodic DNA molecules Journal Article
Em: Physica A: Statistical Mechanics and its Applications, vol. 387, não 22, pp. 5477–5482, 2008.
Resumo | Links | BibTeX | Tags: DNA sequences, Fibonacci, nonextensive
@article{moreira2008low,
title = {Low-temperature specific heat spectra considering nonextensive long-range correlated quasiperiodic DNA molecules},
author = {Moreira, DA and Albuquerque, EL and da Silva, LR and Galvao, DS},
url = {http://www.sciencedirect.com/science/article/pii/S0378437108005347},
year = {2008},
date = {2008-01-01},
journal = {Physica A: Statistical Mechanics and its Applications},
volume = {387},
number = {22},
pages = {5477--5482},
publisher = {North-Holland},
abstract = {We consider the low-temperature specific heat spectra of long-range correlated quasiperiodic DNA molecules using a q-gaussian distribution, and compare them with those considering the Boltzmann-Gibbs distribution. The energy spectra are calculated using the one-dimensional Schrödinger equation in a tight-binding approximation with the on-site energy exhibiting long-range disorder and non-random hopping amplitudes. We focus our attention at the low temperature region, where the specific heat spectra presents a logarithmic-periodic oscillations as a function of the temperature T around a mean value given by a characteristic dimension of the energy spectrum.},
keywords = {DNA sequences, Fibonacci, nonextensive},
pubstate = {published},
tppubtype = {article}
}
We consider the low-temperature specific heat spectra of long-range correlated quasiperiodic DNA molecules using a q-gaussian distribution, and compare them with those considering the Boltzmann-Gibbs distribution. The energy spectra are calculated using the one-dimensional Schrödinger equation in a tight-binding approximation with the on-site energy exhibiting long-range disorder and non-random hopping amplitudes. We focus our attention at the low temperature region, where the specific heat spectra presents a logarithmic-periodic oscillations as a function of the temperature T around a mean value given by a characteristic dimension of the energy spectrum.


