http://scholar.google.com/citations?hl=en&user=95SvbM8AAAAJ
1.
Hall, Lee J; Coluci, Vitor R; Galvao, Douglas S; Kozlov, Mikhail E; Zhang, Mei; Dantas, Socrates O; Baughman, Ray H
Sign change of Poisson's ratio for carbon nanotube sheets Journal Article
Em: Science, vol. 320, não 5875, pp. 504–507, 2008.
@article{hall2008sign,
title = {Sign change of Poisson's ratio for carbon nanotube sheets},
author = {Hall, Lee J and Coluci, Vitor R and Galvao, Douglas S and Kozlov, Mikhail E and Zhang, Mei and Dantas, Socrates O and Baughman, Ray H},
url = {http://www.sciencemag.org/content/320/5875/504.short},
year = {2008},
date = {2008-01-01},
journal = {Science},
volume = {320},
number = {5875},
pages = {504--507},
publisher = {American Association for the Advancement of Science},
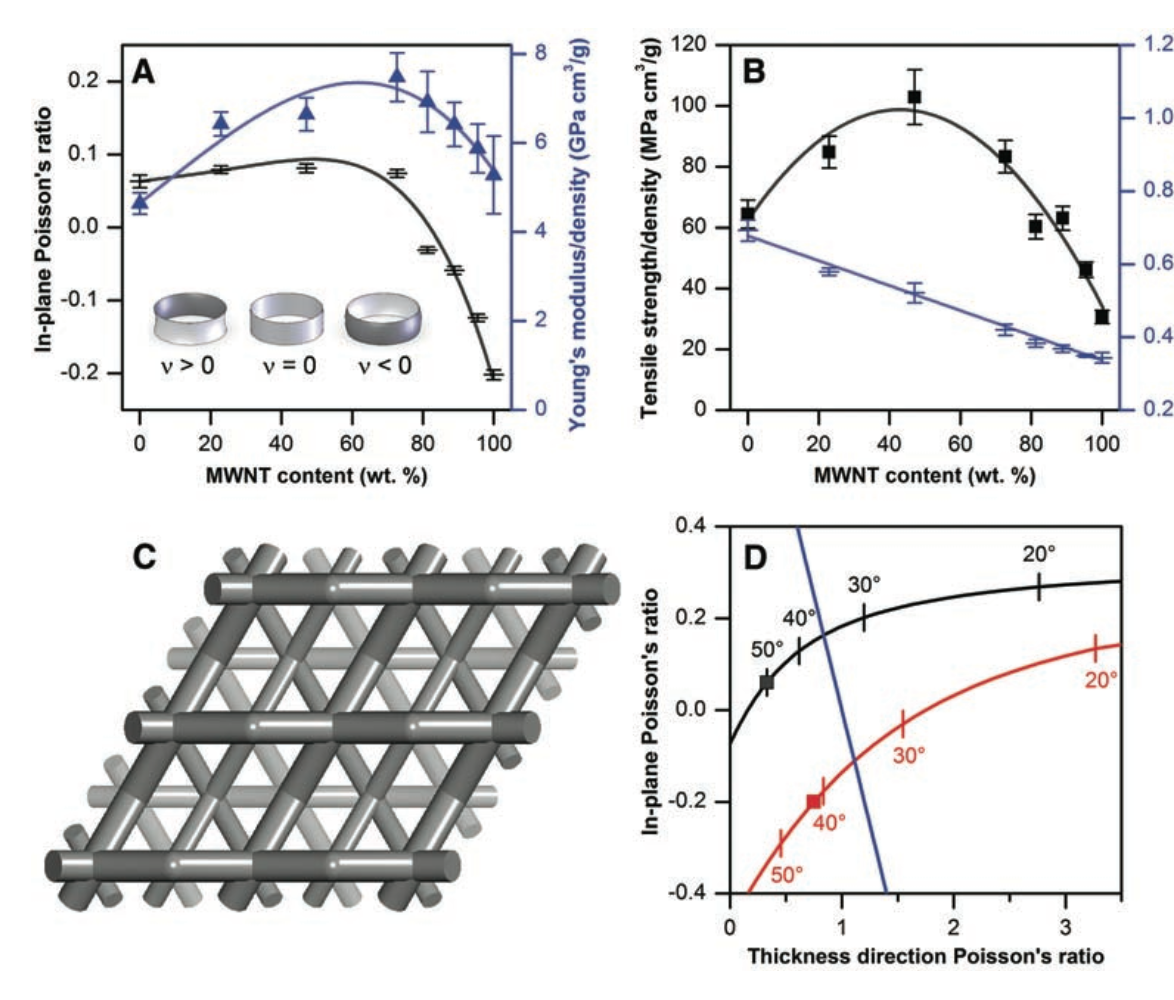
abstract = {Most materials shrink laterally like a rubber band when stretched, so their Poisson's ratios are positive. Likewise, most materials contract in all directions when hydrostatically compressed and decrease density when stretched, so they have positive linear compressibilities. We found that the in-plane Poisson's ratio of carbon nanotube sheets (buckypaper) can be tuned from positive to negative by mixing single-walled and multiwalled nanotubes. Density-normalized sheet toughness, strength, and modulus were substantially increased by this mixing. A simple model predicts the sign and magnitude of Poisson's ratio for buckypaper from the relative ease of nanofiber bending and stretch, and explains why the Poisson's ratios of ordinary writing paper are positive and much larger. Theory also explains why the negative in-plane Poisson's ratio is associated with a large positive Poisson's ratio for the sheet thickness, and predicts that hydrostatic compression can produce biaxial sheet expansion. This tunability of Poisson's ratio can be exploited in the design of sheet-derived composites, artificial muscles, gaskets, and chemical and mechanical sensors.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Most materials shrink laterally like a rubber band when stretched, so their Poisson's ratios are positive. Likewise, most materials contract in all directions when hydrostatically compressed and decrease density when stretched, so they have positive linear compressibilities. We found that the in-plane Poisson's ratio of carbon nanotube sheets (buckypaper) can be tuned from positive to negative by mixing single-walled and multiwalled nanotubes. Density-normalized sheet toughness, strength, and modulus were substantially increased by this mixing. A simple model predicts the sign and magnitude of Poisson's ratio for buckypaper from the relative ease of nanofiber bending and stretch, and explains why the Poisson's ratios of ordinary writing paper are positive and much larger. Theory also explains why the negative in-plane Poisson's ratio is associated with a large positive Poisson's ratio for the sheet thickness, and predicts that hydrostatic compression can produce biaxial sheet expansion. This tunability of Poisson's ratio can be exploited in the design of sheet-derived composites, artificial muscles, gaskets, and chemical and mechanical sensors.
2008
1.
Hall, Lee J; Coluci, Vitor R; Galvao, Douglas S; Kozlov, Mikhail E; Zhang, Mei; Dantas, Socrates O; Baughman, Ray H
Sign change of Poisson's ratio for carbon nanotube sheets Journal Article
Em: Science, vol. 320, não 5875, pp. 504–507, 2008.
Resumo | Links | BibTeX | Tags: Artificial Muscles, Auxetics, Carbon Nanotube Forests, sheets, top20
@article{hall2008sign,
title = {Sign change of Poisson's ratio for carbon nanotube sheets},
author = {Hall, Lee J and Coluci, Vitor R and Galvao, Douglas S and Kozlov, Mikhail E and Zhang, Mei and Dantas, Socrates O and Baughman, Ray H},
url = {http://www.sciencemag.org/content/320/5875/504.short},
year = {2008},
date = {2008-01-01},
journal = {Science},
volume = {320},
number = {5875},
pages = {504--507},
publisher = {American Association for the Advancement of Science},
abstract = {Most materials shrink laterally like a rubber band when stretched, so their Poisson's ratios are positive. Likewise, most materials contract in all directions when hydrostatically compressed and decrease density when stretched, so they have positive linear compressibilities. We found that the in-plane Poisson's ratio of carbon nanotube sheets (buckypaper) can be tuned from positive to negative by mixing single-walled and multiwalled nanotubes. Density-normalized sheet toughness, strength, and modulus were substantially increased by this mixing. A simple model predicts the sign and magnitude of Poisson's ratio for buckypaper from the relative ease of nanofiber bending and stretch, and explains why the Poisson's ratios of ordinary writing paper are positive and much larger. Theory also explains why the negative in-plane Poisson's ratio is associated with a large positive Poisson's ratio for the sheet thickness, and predicts that hydrostatic compression can produce biaxial sheet expansion. This tunability of Poisson's ratio can be exploited in the design of sheet-derived composites, artificial muscles, gaskets, and chemical and mechanical sensors.},
keywords = {Artificial Muscles, Auxetics, Carbon Nanotube Forests, sheets, top20},
pubstate = {published},
tppubtype = {article}
}
Most materials shrink laterally like a rubber band when stretched, so their Poisson's ratios are positive. Likewise, most materials contract in all directions when hydrostatically compressed and decrease density when stretched, so they have positive linear compressibilities. We found that the in-plane Poisson's ratio of carbon nanotube sheets (buckypaper) can be tuned from positive to negative by mixing single-walled and multiwalled nanotubes. Density-normalized sheet toughness, strength, and modulus were substantially increased by this mixing. A simple model predicts the sign and magnitude of Poisson's ratio for buckypaper from the relative ease of nanofiber bending and stretch, and explains why the Poisson's ratios of ordinary writing paper are positive and much larger. Theory also explains why the negative in-plane Poisson's ratio is associated with a large positive Poisson's ratio for the sheet thickness, and predicts that hydrostatic compression can produce biaxial sheet expansion. This tunability of Poisson's ratio can be exploited in the design of sheet-derived composites, artificial muscles, gaskets, and chemical and mechanical sensors.


