My research interests are:
- Strongly correlated electron systems, such as heavy fermion compounds, transition metal oxides, and others.
- Disordered systems such as doped semiconductors.
- Strongly correlated disordered systems.
Some highlights of my recent research are described below.
The metal-insulator transition
Materials can be classified as metals or insulators, depending on whether they conduct electric currents or not. Both types of materials find important applications in electronic devices: electric contacts are made of good metals such as copper and good capacitors usually employ good insulators. Besides, computer processors are full of transistors, whose functionality depends on the possibility of turning metals into insulators and vice-versa through the application of a voltage. However, the physics of this transmutation, the so-called metal-insulator transition, is not completely understood.
Two important mechanisms that can turn metals into insulators are disorder and strong interactions. Disorder means that the usual periodic order of pristine crystals is disrupted by imperfections. Such imperfections sometimes trap all the electrons responsible for electric conduction and transform a metal into an insulator. By strong interactions we mean that in compounds that contain certain elements like transition metals (like Fe) or rare earths (like Ce), the effects of the electric repulsion between the electrons can be so large that even their ability to conduct electricity is impaired: they become jammed in the atoms and do not flow in electric currents. Each of these mechanisms presents a major challenge to our understanding and the situation becomes even worse when both play a role. I have devoted a lot of effort to understanding this interplay. It can generate unexpected effects.
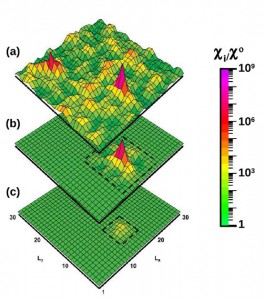
For example, strongly interacting electrons in a disordered system can form a “rough spatial landscape” of behaviors. Some regions of this landscape, for example, can exhibit a strong response to an external magnetic field: they behave like tiny magnets that easily line up along the applied field. We have been able to determine the sizes of these magnetic regions and have shown that their response to an applied magnetic field can vary by many orders of magnitude as the sample is scanned. The top panel on the left (a) shows the spatial variations of the magnetic response. The lower panels show the size of the “largest peak”: if the box in (b) is cropped from the rest of the sample in (a), the peak survives; a smaller box, as in (c), destroys it.
Electronic Griffiths phase of the d=2 Mott transition, E. C. Andrade, E. Miranda, and V. Dobrosavljević, Phys. Rev. Lett. 102, 206403 (2009).
Impurities in strongly correlated metals and superconductors
Besides the global role of imperfections in crystals, there is interest in understanding how the electron liquid in metals and superconductors is perturbed microscopically in the near vicinity of an impurity. The unprecedented fine detail with which researchers can probe matter at the nanoscale prompts us to investigate how the strong repulsion between electrons modifies the behavior of less correlated materials. In the latter case of weakly interacting metals (such as elemental copper, for example), the spatial variation of the electronic density around an impurity makes apparent the “wave-like” nature of quantum particles: these are the so-called Friedel oscillations (see a picture here, for subscribers). How is this picture changed when the material is more strongly interacting?
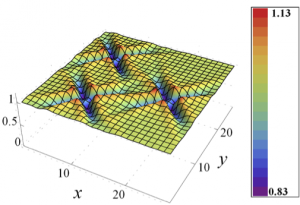
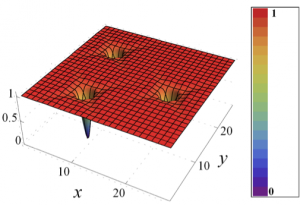
In the top panel of the figure on the left, we show the Friedel oscillations of the electron density around an impurity in a weakly correlated material. The oscillations die away very slowly and extend to regions far from the center. The peculiar “cross-shaped” pattern reflects the particular characteristics of the metal excitation spectra. When the strong interactions are cranked up, however, the oscillations are strongly suppressed and become confined to a small region close to the impurity. In a very real sense, the electron fluid becomes more “rigid” and less deformable by the imperfection.
Quantum ripples in strongly correlated metals, E. C. Andrade, E. Miranda, and V. Dobrosavljević, Phys. Rev. Lett. 104, 236401 (2010).
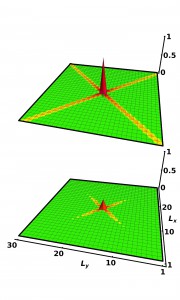
Interestingly, something very similar occurs even in superconductors. Superconductors are special states of matter in which a material is able to conduct an electric current without any resistance! The so-called superconducting order parameter serves as a measure of the “strength” of superconductivity. It too can be perturbed by lattice imperfections. In fact, sufficient disorder can destroy superconductivity altogether. In the micro-region around an impurity in a conventional superconductor, the order parameter is deformed, as shown in the left panel of the figure below. In a strongly interacting superconductor (right panel of the figure below), the perturbation is much less severe.
Mottness-induced healing in strongly correlated superconductors (Supplemental Material), Shao Tang, E. Miranda, V. Dobrosavljević, Phys. Rev. B 91, 020501(R) (2015).
