1.
Vasconcelos, MS; Azevedo, David L; Hadad, A; Galvao, DS
Electronic properties of Fibonacci and random Si--Ge chains Journal Article
In: Journal of Physics: Condensed Matter, vol. 23, no. 40, pp. 405501, 2011.
@article{vasconcelos2011electronic,
title = {Electronic properties of Fibonacci and random Si--Ge chains},
author = {Vasconcelos, MS and Azevedo, David L and Hadad, A and Galvao, DS},
url = {http://iopscience.iop.org/0953-8984/23/40/405501},
year = {2011},
date = {2011-01-01},
journal = {Journal of Physics: Condensed Matter},
volume = {23},
number = {40},
pages = {405501},
publisher = {IOP Publishing},
abstract = {In this paper we address a theoretical calculation of the electronic spectra of an Si–Ge atomic chain that is arranged in a Fibonacci quasi-periodic sequence, by using a semi-empirical quantum method based on the Hückel extended model. We apply the Fibonacci substitutional sequences in the atomic building blocks A(Si) and B(Ge) through the inflation rule or a recursion relation. In our ab initio calculations we use only a single point, which is sufficient for considering all the orbitals and charge distribution across the entire system. Although the calculations presented here are more complete than the models adopted in the literature which take into account the electronic interaction only up to the second and third neighbors, an interesting property remains in their electronic spectra: the fractality (which is the main signature of this kind of system). We discuss this fractality of the spectra and we compare them with the random arrangement of the Si–Ge atomic chain, and with previous results based on the tight-binding approximation of the Schrödinger equation considering up to the nearest neighbor.
},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
In this paper we address a theoretical calculation of the electronic spectra of an Si–Ge atomic chain that is arranged in a Fibonacci quasi-periodic sequence, by using a semi-empirical quantum method based on the Hückel extended model. We apply the Fibonacci substitutional sequences in the atomic building blocks A(Si) and B(Ge) through the inflation rule or a recursion relation. In our ab initio calculations we use only a single point, which is sufficient for considering all the orbitals and charge distribution across the entire system. Although the calculations presented here are more complete than the models adopted in the literature which take into account the electronic interaction only up to the second and third neighbors, an interesting property remains in their electronic spectra: the fractality (which is the main signature of this kind of system). We discuss this fractality of the spectra and we compare them with the random arrangement of the Si–Ge atomic chain, and with previous results based on the tight-binding approximation of the Schrödinger equation considering up to the nearest neighbor.
2.
Moreira, DA; Albuquerque, EL; da Silva, LR; Galvao, DS
Low-temperature specific heat spectra considering nonextensive long-range correlated quasiperiodic DNA molecules Journal Article
In: Physica A: Statistical Mechanics and its Applications, vol. 387, no. 22, pp. 5477–5482, 2008.
@article{moreira2008low,
title = {Low-temperature specific heat spectra considering nonextensive long-range correlated quasiperiodic DNA molecules},
author = {Moreira, DA and Albuquerque, EL and da Silva, LR and Galvao, DS},
url = {http://www.sciencedirect.com/science/article/pii/S0378437108005347},
year = {2008},
date = {2008-01-01},
journal = {Physica A: Statistical Mechanics and its Applications},
volume = {387},
number = {22},
pages = {5477--5482},
publisher = {North-Holland},
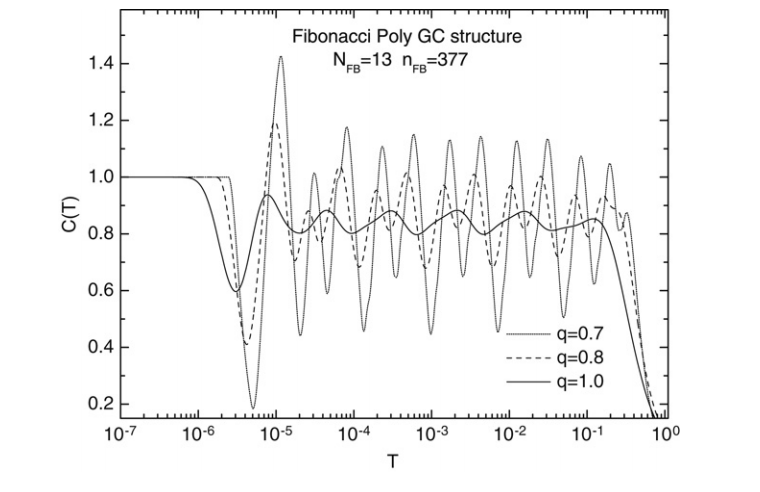
abstract = {We consider the low-temperature specific heat spectra of long-range correlated quasiperiodic DNA molecules using a q-gaussian distribution, and compare them with those considering the Boltzmann-Gibbs distribution. The energy spectra are calculated using the one-dimensional Schrödinger equation in a tight-binding approximation with the on-site energy exhibiting long-range disorder and non-random hopping amplitudes. We focus our attention at the low temperature region, where the specific heat spectra presents a logarithmic-periodic oscillations as a function of the temperature T around a mean value given by a characteristic dimension of the energy spectrum.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
We consider the low-temperature specific heat spectra of long-range correlated quasiperiodic DNA molecules using a q-gaussian distribution, and compare them with those considering the Boltzmann-Gibbs distribution. The energy spectra are calculated using the one-dimensional Schrödinger equation in a tight-binding approximation with the on-site energy exhibiting long-range disorder and non-random hopping amplitudes. We focus our attention at the low temperature region, where the specific heat spectra presents a logarithmic-periodic oscillations as a function of the temperature T around a mean value given by a characteristic dimension of the energy spectrum.
2011
2.
Vasconcelos, MS; Azevedo, David L; Hadad, A; Galvao, DS
Electronic properties of Fibonacci and random Si--Ge chains Journal Article
In: Journal of Physics: Condensed Matter, vol. 23, no. 40, pp. 405501, 2011.
Abstract | Links | BibTeX | Tags: Electronic Structure, Fibonacci, Si-Ge chains
@article{vasconcelos2011electronic,
title = {Electronic properties of Fibonacci and random Si--Ge chains},
author = {Vasconcelos, MS and Azevedo, David L and Hadad, A and Galvao, DS},
url = {http://iopscience.iop.org/0953-8984/23/40/405501},
year = {2011},
date = {2011-01-01},
journal = {Journal of Physics: Condensed Matter},
volume = {23},
number = {40},
pages = {405501},
publisher = {IOP Publishing},
abstract = {In this paper we address a theoretical calculation of the electronic spectra of an Si–Ge atomic chain that is arranged in a Fibonacci quasi-periodic sequence, by using a semi-empirical quantum method based on the Hückel extended model. We apply the Fibonacci substitutional sequences in the atomic building blocks A(Si) and B(Ge) through the inflation rule or a recursion relation. In our ab initio calculations we use only a single point, which is sufficient for considering all the orbitals and charge distribution across the entire system. Although the calculations presented here are more complete than the models adopted in the literature which take into account the electronic interaction only up to the second and third neighbors, an interesting property remains in their electronic spectra: the fractality (which is the main signature of this kind of system). We discuss this fractality of the spectra and we compare them with the random arrangement of the Si–Ge atomic chain, and with previous results based on the tight-binding approximation of the Schrödinger equation considering up to the nearest neighbor.
},
keywords = {Electronic Structure, Fibonacci, Si-Ge chains},
pubstate = {published},
tppubtype = {article}
}
In this paper we address a theoretical calculation of the electronic spectra of an Si–Ge atomic chain that is arranged in a Fibonacci quasi-periodic sequence, by using a semi-empirical quantum method based on the Hückel extended model. We apply the Fibonacci substitutional sequences in the atomic building blocks A(Si) and B(Ge) through the inflation rule or a recursion relation. In our ab initio calculations we use only a single point, which is sufficient for considering all the orbitals and charge distribution across the entire system. Although the calculations presented here are more complete than the models adopted in the literature which take into account the electronic interaction only up to the second and third neighbors, an interesting property remains in their electronic spectra: the fractality (which is the main signature of this kind of system). We discuss this fractality of the spectra and we compare them with the random arrangement of the Si–Ge atomic chain, and with previous results based on the tight-binding approximation of the Schrödinger equation considering up to the nearest neighbor.
2008
1.
Moreira, DA; Albuquerque, EL; da Silva, LR; Galvao, DS
Low-temperature specific heat spectra considering nonextensive long-range correlated quasiperiodic DNA molecules Journal Article
In: Physica A: Statistical Mechanics and its Applications, vol. 387, no. 22, pp. 5477–5482, 2008.
Abstract | Links | BibTeX | Tags: DNA sequences, Fibonacci, nonextensive
@article{moreira2008low,
title = {Low-temperature specific heat spectra considering nonextensive long-range correlated quasiperiodic DNA molecules},
author = {Moreira, DA and Albuquerque, EL and da Silva, LR and Galvao, DS},
url = {http://www.sciencedirect.com/science/article/pii/S0378437108005347},
year = {2008},
date = {2008-01-01},
journal = {Physica A: Statistical Mechanics and its Applications},
volume = {387},
number = {22},
pages = {5477--5482},
publisher = {North-Holland},
abstract = {We consider the low-temperature specific heat spectra of long-range correlated quasiperiodic DNA molecules using a q-gaussian distribution, and compare them with those considering the Boltzmann-Gibbs distribution. The energy spectra are calculated using the one-dimensional Schrödinger equation in a tight-binding approximation with the on-site energy exhibiting long-range disorder and non-random hopping amplitudes. We focus our attention at the low temperature region, where the specific heat spectra presents a logarithmic-periodic oscillations as a function of the temperature T around a mean value given by a characteristic dimension of the energy spectrum.},
keywords = {DNA sequences, Fibonacci, nonextensive},
pubstate = {published},
tppubtype = {article}
}
We consider the low-temperature specific heat spectra of long-range correlated quasiperiodic DNA molecules using a q-gaussian distribution, and compare them with those considering the Boltzmann-Gibbs distribution. The energy spectra are calculated using the one-dimensional Schrödinger equation in a tight-binding approximation with the on-site energy exhibiting long-range disorder and non-random hopping amplitudes. We focus our attention at the low temperature region, where the specific heat spectra presents a logarithmic-periodic oscillations as a function of the temperature T around a mean value given by a characteristic dimension of the energy spectrum.
http://scholar.google.com/citations?hl=en&user=95SvbM8AAAAJ
