1.
Fonseca, AD; Malta, CP; Galvao, DS
Elastic Properties of Normal and Binormal Helical Nanowires Proceedings
Warrendale, Pa.; Materials Research Society; 1999, vol. 963, 2007.
@proceedings{fonseca2007elastic,
title = {Elastic Properties of Normal and Binormal Helical Nanowires},
author = {Fonseca, AD and Malta, CP and Galvao, DS},
url = {http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=8026852},
year = {2007},
date = {2007-01-01},
journal = {MATERIALS RESEARCH SOCIETY SYMPOSIUM PROCEEDINGS},
volume = {963},
pages = {88},
publisher = {Warrendale, Pa.; Materials Research Society; 1999},
abstract = {A helical nanowire can be defined as being a nanoscopic rod whose axis follows a helical curve in space. In the case of a nanowire with asymmetric cross section, the helical nanostructure can be classified as normal or binormal helix, according to the orientation of the cross section with respect to the helical axis of the structure. In this work, we present a simple model to study the elastic properties of a helical nanowire with asymmetric cross section. We use the framework of the Kirchhoff rod model to obtain an expression relating the Hooke's constant, h, of normal and binormal nanohelices to their geometric features. We also obtain the Young's modulus values. These relations can be used by experimentalists to evaluate the elastic properties of helical nanostructures. We showed that the Hooke's constant of a normal nanohelix is higher than that of a binormal one. We illustrate our results using experimentally obtained nanohelices reported in the literature.},
keywords = {},
pubstate = {published},
tppubtype = {proceedings}
}
A helical nanowire can be defined as being a nanoscopic rod whose axis follows a helical curve in space. In the case of a nanowire with asymmetric cross section, the helical nanostructure can be classified as normal or binormal helix, according to the orientation of the cross section with respect to the helical axis of the structure. In this work, we present a simple model to study the elastic properties of a helical nanowire with asymmetric cross section. We use the framework of the Kirchhoff rod model to obtain an expression relating the Hooke's constant, h, of normal and binormal nanohelices to their geometric features. We also obtain the Young's modulus values. These relations can be used by experimentalists to evaluate the elastic properties of helical nanostructures. We showed that the Hooke's constant of a normal nanohelix is higher than that of a binormal one. We illustrate our results using experimentally obtained nanohelices reported in the literature.
2.
Fonseca, Alexandre F; Malta, CP; Galvao, DS
Is it possible to grow amorphous normal nanosprings? Journal Article
In: Nanotechnology, vol. 18, no. 43, pp. 435606, 2007.
@article{fonseca2007possible,
title = {Is it possible to grow amorphous normal nanosprings?},
author = {Fonseca, Alexandre F and Malta, CP and Galvao, DS},
url = {http://iopscience.iop.org/0957-4484/18/43/435606},
year = {2007},
date = {2007-01-01},
journal = {Nanotechnology},
volume = {18},
number = {43},
pages = {435606},
publisher = {IOP Publishing},
abstract = {Nanosprings have been objects of intense investigations in recent years. They can be classified as normal or binormal depending on the geometry of their cross-section. As normal amorphous nanosprings have not yet been observed experimentally, we have decided to investigate this matter. We discuss the shape of the catalyst in terms of the cross-sectional shape of the nanospring and show that, within the vapor–liquid–solid model, the growth of amorphous binormal nanosprings is energetically favored.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Nanosprings have been objects of intense investigations in recent years. They can be classified as normal or binormal depending on the geometry of their cross-section. As normal amorphous nanosprings have not yet been observed experimentally, we have decided to investigate this matter. We discuss the shape of the catalyst in terms of the cross-sectional shape of the nanospring and show that, within the vapor–liquid–solid model, the growth of amorphous binormal nanosprings is energetically favored.
2007
2.
Fonseca, AD; Malta, CP; Galvao, DS
Elastic Properties of Normal and Binormal Helical Nanowires Proceedings
Warrendale, Pa.; Materials Research Society; 1999, vol. 963, 2007.
Abstract | Links | BibTeX | Tags: Elasticity, Helical Structures, Mechanical Properties, Nanowires
@proceedings{fonseca2007elastic,
title = {Elastic Properties of Normal and Binormal Helical Nanowires},
author = {Fonseca, AD and Malta, CP and Galvao, DS},
url = {http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=8026852},
year = {2007},
date = {2007-01-01},
journal = {MATERIALS RESEARCH SOCIETY SYMPOSIUM PROCEEDINGS},
volume = {963},
pages = {88},
publisher = {Warrendale, Pa.; Materials Research Society; 1999},
abstract = {A helical nanowire can be defined as being a nanoscopic rod whose axis follows a helical curve in space. In the case of a nanowire with asymmetric cross section, the helical nanostructure can be classified as normal or binormal helix, according to the orientation of the cross section with respect to the helical axis of the structure. In this work, we present a simple model to study the elastic properties of a helical nanowire with asymmetric cross section. We use the framework of the Kirchhoff rod model to obtain an expression relating the Hooke's constant, h, of normal and binormal nanohelices to their geometric features. We also obtain the Young's modulus values. These relations can be used by experimentalists to evaluate the elastic properties of helical nanostructures. We showed that the Hooke's constant of a normal nanohelix is higher than that of a binormal one. We illustrate our results using experimentally obtained nanohelices reported in the literature.},
keywords = {Elasticity, Helical Structures, Mechanical Properties, Nanowires},
pubstate = {published},
tppubtype = {proceedings}
}
A helical nanowire can be defined as being a nanoscopic rod whose axis follows a helical curve in space. In the case of a nanowire with asymmetric cross section, the helical nanostructure can be classified as normal or binormal helix, according to the orientation of the cross section with respect to the helical axis of the structure. In this work, we present a simple model to study the elastic properties of a helical nanowire with asymmetric cross section. We use the framework of the Kirchhoff rod model to obtain an expression relating the Hooke's constant, h, of normal and binormal nanohelices to their geometric features. We also obtain the Young's modulus values. These relations can be used by experimentalists to evaluate the elastic properties of helical nanostructures. We showed that the Hooke's constant of a normal nanohelix is higher than that of a binormal one. We illustrate our results using experimentally obtained nanohelices reported in the literature.
1.
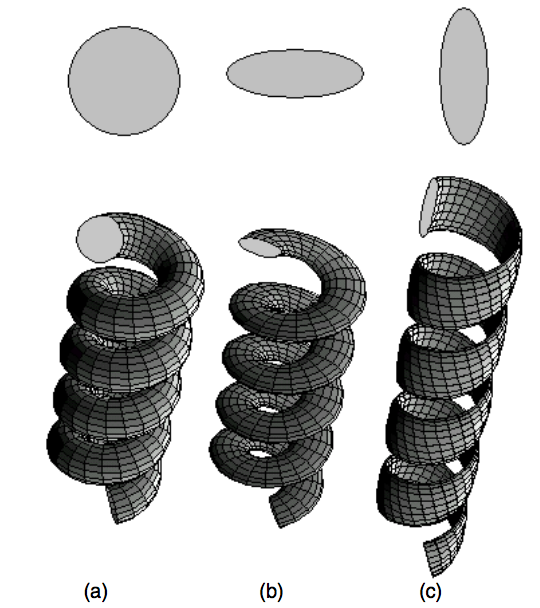
Fonseca, Alexandre F; Malta, CP; Galvao, DS
Is it possible to grow amorphous normal nanosprings? Journal Article
In: Nanotechnology, vol. 18, no. 43, pp. 435606, 2007.
Abstract | Links | BibTeX | Tags: Elasticity, Helical Structures, Mechanical Properties, Nanowires
@article{fonseca2007possible,
title = {Is it possible to grow amorphous normal nanosprings?},
author = {Fonseca, Alexandre F and Malta, CP and Galvao, DS},
url = {http://iopscience.iop.org/0957-4484/18/43/435606},
year = {2007},
date = {2007-01-01},
journal = {Nanotechnology},
volume = {18},
number = {43},
pages = {435606},
publisher = {IOP Publishing},
abstract = {Nanosprings have been objects of intense investigations in recent years. They can be classified as normal or binormal depending on the geometry of their cross-section. As normal amorphous nanosprings have not yet been observed experimentally, we have decided to investigate this matter. We discuss the shape of the catalyst in terms of the cross-sectional shape of the nanospring and show that, within the vapor–liquid–solid model, the growth of amorphous binormal nanosprings is energetically favored.},
keywords = {Elasticity, Helical Structures, Mechanical Properties, Nanowires},
pubstate = {published},
tppubtype = {article}
}
Nanosprings have been objects of intense investigations in recent years. They can be classified as normal or binormal depending on the geometry of their cross-section. As normal amorphous nanosprings have not yet been observed experimentally, we have decided to investigate this matter. We discuss the shape of the catalyst in terms of the cross-sectional shape of the nanospring and show that, within the vapor–liquid–solid model, the growth of amorphous binormal nanosprings is energetically favored.
http://scholar.google.com/citations?hl=en&user=95SvbM8AAAAJ
