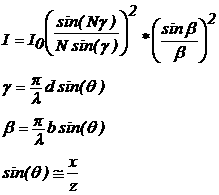4 – Difração da luz por Fendas

1 – INTRODUÇÃO

Difração é o nome genérico dado aos fenômenos associados a desvios da propagação da luz em relação ao previsto pela óptica geométrica.

O efeito de difração é observado para todos os tipos de ondas. Nas condições rotineiras raramente observamos a difração da luz. Entretanto, a difração das ondas sonoras é difícil de ser evitada. O som contorna obstáculos de tamanhos razoáveis tais como as mobílias de uma sala e preenchem todo o ambiente de maneira mais ou menos uniforme. Esta diferença observada entre a difração das ondas sonoras e ondas luminosas é devida à diferença entre os respectivos comprimentos de onda. O comprimento de onda do som é da ordem de 1 m, enquanto que o da luz visível é da ordem de 5 x 10-7 m.

Os efeitos de difração são apreciáveis quando os obstáculos ou aberturas são de dimensões comparáveis ao comprimento de onda

.

a) Difração de fenda simples

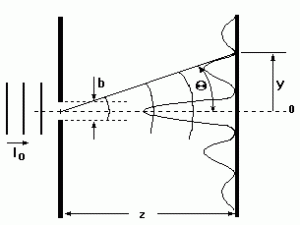
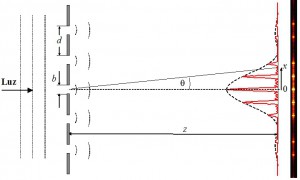
Fig.1 – Difração de fenda simples.

Na fig.1 um feixe de luz monocromática passa por uma fenda de largura b e atinge um anteparo a uma distância z.

As ondas de Huygens originárias em cada ponto da abertura interferem entre si e produzem o padrão de difração ilustrado nesta figura. Observamos um máximo central e pontos onde a intensidade luminosa é nula

.

b) Difração de Fenda dupla

Um arranjo semelhante pode ser feito para se observar a difração de fenda dupla. O efeito de difração observado quando a luz passa por cada uma das fendas é o mesmo discutido anteriormente, mas o resultado final em qualquer direção depende da diferença de caminho entre as duas contribuições

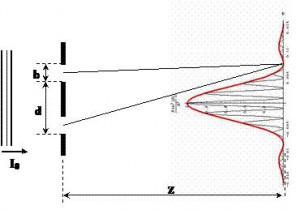                                                       Fig. 2 – Difração de fenda dupla.

A fig. 2 nos mostra que a luz difratada pelas duas fendas sofre efeito de interferência, de modo a se obter no anteparo máximos e mínimos de luz.

A intensidade total é o produto de um fator devido à difração de fenda simples(sinb/b) vezes um fator devido à interferência de fenda dupla (cos (γ)).   O fator de interferência tem um máximo (chamados de máximos principais) sempre que: 

d sin (Θ) = m λ      onde m=0,1,2,3,4, ...denota a ordem do padrão. 

Já o fator de difração tem mínimos de intensidade sempre que:

b sin (Θ) = n λ       onde n=1,2,3,4, ... denota a ordem do mínimo.

O padrão pode ser descrito dizendo-se que o fator de difração “modula” as variações do fator de interferência. Sempre que um máximo de interferência coincide espacialmente com um mínimo de difração, esse máximo de interferência é suprimido. Assim, sempre que   (d/a) n = m   um máximo do padrão de interferência será eliminado

 

c) Difração de fenda múltipla

Fig. 3 – Difração de N fendas de largura b período d. A linha serrilhada representa a função de difração  (sinb/b)2 . Utilizando a relação apresentada no parágrafo anterior para o caso da fenda dupla, e a relação trigonométrica, o padrão de  intensidades para a fenda dupla pode ser escrito como: 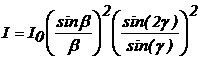  A generalização desta expressão ao casso de Nfendas não é uma tarefa matemática simples. O resultado final, contudo, é bastante simples sendo obtido apenas  substituindo-se  por : Assim para a difração por um arranjo de múltiplas fendas, a distribuição de intensidades é dada por:

2 – OBJETIVOS :

– Observar os efeitos de difração de Fraunhofer produzidos por uma fenda e os efeitos de interferência produzidos por duas ou mais fendas.

– Elaborar um modelo que explique as principais características do padrão de interferência e/ou difração observado.

Verificar quantitativamente as previsões do modelo.

3 – PREPARAÇÃO

a – Estude ou revise os conceitos de interferência e difração, principalmente os seguintes pontos:

a.1 – Experimento de Young.

a.2 – Difração.

a.3 – Difração de Fraunhofer de uma fenda.

a.4 – Difração e interferência por fendas múltiplas – rede de difração

b – para explicar quantitativamente o padrão de difração de uma fenda de abertura b, observado em um anteparo a uma distância z, produzida por ondas incidentes planas, de comprimento de onda l e irradiância I₀ .

b.1 – Mostre que a condição para que o padrão de difração possa ser considerado como de Fraunhofer é :       (b² / 2z) << λ   (1)

b.2 – Mostre que nesta condição o padrão de difração pode ser descrito em termos de irradiância como:      I = Io ( senβ/β) ²     (2)    onde I₀ é a irradiância em y = 0     e

 β = 1/2 Kb sen Θ   (3)

com k=2p /λ e tan Θ = y/z. Note que para y = 0 este modelo prevê o máximo absoluto (ou máximo central) da irradiância.

b.3 – Se b é 1mm e   λ = 633 nm, à partir de qual distância z você espera que a eq. (2) seja válida ?

b.4 – Baseado neste modelo, onde você espera achar os primeiros 4 mínimos de difração?

b.5 – Utilizando algum software de sua preferência simule o experimento obtendo um gráfico de I/ I₀ versus y para λ = 633nm, b = 0.2mm e z = 3m.

Quanto é aproximadamente a intensidade relativa dos primeiros 10 máximos ?

 

c – Estude o modelo para a interferência de duas fendas com largura b e distância entre fendas h (Experimento de Young) levando em consideração os efeitos de difração.

c.1 – Mostre que se a condição de difração de Fraunhofer for satisfeita, a incidência pode ser escrita como:

                                           I = Io cos² γ (sen² β/β²)  (4)      onde  γ = 1/2 kh sen Θ

.

c.2 – Simule no computador o padrão para λ = 633 nm, b = 0.2 mm, z = 3 m e h = 0.5 mm. Determine a posição dos máximos e mínimos de interferência e de difração.

.

d – Generalize o modelo para o caso de N fendas.

d.1 – Mostre que :     I = Io ( senβ/β)² (senNγ/Nsenγ)²   (5).

Verifique que a eq.(5) coincide com a eq. (4) para N = 2.

d.2 – Simule no computador o padrão previsto para N = 3, 4, 5, 10.

Que acontece com a largura dos máximos de interferência, à medida que aumenta N ?

Quantos mínimos de interferência ha dentro do máximo central de difração ( i. é, –p < b < p ) ?

4 – PROCEDIMENTO EXPERIMENTAL (veja o resumo das atividades para este semestre)

Os experimentos serão realizados com um Laser de λ  desconhecido (cuidado, no laboratório tem laser vermelho, laranja, azul e verde). As fendas foram feitas em um filme de cromo sobre vidro. A largura das fendas b e a separação entre elas d são desconhecidos, mas da ordem de:  30 <  b < 60 μm e    60 <  d μm

Alinhamento Para que as medidas sejam feitas com precisão, é fundamental que a máscara com as fendas seja colocada perpendicular ao feixe do Laser, isso pode ser facilmente feito enviando o feixe do Laser refletido na superfície do slide, novamente para a saída do Laser.

Medida do espectro angular de espalhamento para 3 situações:

 

Fenda única, fio de cabelo, e rede de difração.

Medir o espectro ângular, significa medir a intensidade da luz em função do ângulo de observação.

Para esta medida o detector se movimentará linearmente sobre um trilho graduado e perpendicular à direção da incidência

do feixe laser. A medida do ângulo ( na posição dos máximos ou mínimos) correspondente à cada posição do fotodetector no trilho, pode ser feita por triangulação ( Distancia Z conhecida).

Usando o microscópio, medir a largura da fenda , a espessura do fio de cabelo , o período e a largura das fendas da rede de difração. Com as informações das 3 situações diferentes ( fenda única, fio de cabelo e grade de difração) determinar o comprimento de onda do laser utilizado.

Roteiro sugerido:

1 – Montar o conjunto Laser, fenda e detetor no trilho. Projete o padrão de difração/interferência sobre o detetor e registre as intensidades ( Trabalhar sempre na região de linearidade do detector, para evitar que a curva fique achatada pela saturação) e distâncias do máximo central.

2 – Caracterize os padrões de difração/interferência para: 1 fenda, 1 fio de cabelo e N fendas ( N é desconhecido), ou seja, meça as posições dos máximos ou mínimos.

 

3 – No caso de 1 fenda, caracterize os padrões de difração obtidos para várias distâncias fenda-anteparo (z) e verifique se a eq. 2 é válida.

4 – Meça diretamente com o microscópio, as dimensões b e d.

5 –  À partir dos seus dados experimentais, traçar a curva de intensidade difratada para cada uma das 3 situações em função do ângulo de observação.

7– Pode-se concluir que a difração/interferência é um método preciso para medir  l? Qual é a precisão do método?

Obs. O prof. definirá os ítens a fazer

.

5 – BIBLIOGRAFIA

1 – G. R. Fowles, “Introduction to Modern Optics“, Holt, Rinehart and Winston, second edition, New York (1975).

2* – John P. McKelvey and H. Grotch, “Fisica 4 “, Harbra – Harper & Row do Brasil, São Paulo, cap26 (1981).

3 – Francis A. Jenkins and Harvey White,” Fundamental of Optics“, MacGraw Hill. (1976).

4 – Hecht, Eugene, “Optics“. Adelphi University, Addison-Wesley Publishing Company (1990)

.

Fig. 14.4 – Figuras de difração produzidas por diferentes números de fendas     d = 3b and N = 1 (superior), N = 2 (centro), and N = 10 (Inferior).

Z (eixo de intensidade) = log[G(y)I(x)/I0 + 10-5] + 5, onde G(y) é a função gaussiana que determina o contorno do feixe laser.

A escala log de intensidade simula a resposta do ôlho para luz intensa. (Simulações: Paulo Dainese e Hugo Fragnito, Nov. 2004).

.

6 – APÊNDICE :

.

a) – DIFRAÇÃO DE UM FIO DE CABELO

Se no lugar de uma fenda simples, colocarmos um fio de cabelo, o padrão de difração produzido por um feixe laser, é muito similar ao da fenda, exceto na pequena região dentro do feixe.

Isto pode ser explicado a partir do principio de Babinet de máscaras complementares. Consideremos duas máscaras complementares como as da figura 14.5, iluminadas em idênticas condições por um feixe de luz.

Sejam E_A e E_B os campos de difração no ponto P produzidos em cada caso: 

EA (P) =  ∫ f(E)ds

onde indica a integral de Huygens.

Fig. 14.5 – A e B Máscaras complementares.

(ou, mais corretamente, a integral de Kirchoff – Fresnel, mas que de todos modos não é necessário especificar a forma desta integral) f(E) é uma função do campo E na superfície da máscara e ds o elemento de área.

A soma das áreas das duas máscaras (A + B) é a superfície sem obstáculos, onde E(P) é o campo produzido na ausência de máximos.

.Portanto, E_A+ E_B = E

Este resultado é o princípio de Babinet. Este princípio é útil principalmente nos pontos onde E(P) = 0, em cujo caso temos E_A = -E_B e portanto, a irradiância I_A = I_B .

No caso do fio de cabelo iluminado por um feixe Laser, o padrão coincide com o da fenda em todos os pontos, exceto na região dentro do feixe (onde E ¹ 0).

.

b) – REGISTRO FOTOGRÁFICO

Também é possível registrar as figuras através do processo fotográfico, colocando-se um papel fotográfico para ser exposto durante um tempo bem controlado, à luz emitida e difratada pelas fendas.

É preciso mencionar que neste caso, a distância papel-fenda deverá ser bem menor uma vez que as dimensões do papel fotográfico são menores, consequentemente a imprecisão nas medidas a serem feitas nas fotos aumenta, aumentando assim o erro das medidas das fendas.

Lembrar também que a distribuição de luz, ao longo da figura de difração não é homogênea,

resultando em uma imagem com muito contraste no centro e quase nada nas laterais. Essa limitação pode ser superada bloqueando a parte central da imagem, expondo mais tempo as regiões laterais da figura.

.

c ) – PARAFUSO MICROMÉTRICO DO MICROSCÓPIO

.

Fig. 14.6 – Escala do microscópio.

A figura 14.6 mostra a escala do parafuso micrométrico do microscópio usado para se medir as fendas.

O parafuso é composto de 3 escalas:

a) Tambor fixo

i – escala vertical em mm

ii – escala horizontal em 0.001mm

b) Tambor móvel

iii – em 0.01mm ( 1mm dividido em 100 partes)

A cada volta completa do parafuso, a mesa se desloca 1,000 mm( Para maiores detalhes veja as fotos que estão no laboratório).

d) DIFRAÇÃO DE UMA FENDA

.

Fig. 14.7a – Figura de difração de uma fenda.Fig. 14.7b – Figura de difração de uma fenda retangular.

e) DISTRIBUIÇÃO DA INTENSIDADE LUMINOSA

.

Fig.14.8 – Figura da distribuição da intensidade luminosa..Fig.14.9 – Microscópio Metrológico e seus comandos.

1 – INTRODUÇÃO

Difração é o nome genérico dado aos fenômenos associados a desvios da propagação da luz em relação ao previsto pela óptica geométrica.

O efeito de difração é observado para todos os tipos de ondas. Nas condições rotineiras raramente observamos a difração da luz. Entretanto, a difração das ondas sonoras é difícil de ser evitada. O som contorna obstáculos de tamanhos razoáveis tais como as mobílias de uma sala e preenchem todo o ambiente de maneira mais ou menos uniforme. Esta diferença observada entre a difração das ondas sonoras e ondas luminosas é devida à diferença entre os respectivos comprimentos de onda. O comprimento de onda do som é da ordem de 1 m, enquanto que o da luz visível é da ordem de 5 x 10-7 m.

Os efeitos de difração são apreciáveis quando os obstáculos ou aberturas são de dimensões comparáveis ao comprimento de onda

.

a) Difração de fenda simples

Fig.14.1 – Difração de fenda simples.

Na fig.14.1 um feixe de luz monocromática passa por uma fenda de largura b e atinge um anteparo a uma distância z.

As ondas de Huygens originárias em cada ponto da abertura interferem entre si e produzem o padrão de difração ilustrado nesta figura. Observamos um máximo central e pontos onde a intensidade luminosa é nula

.

b) Difração de Fenda dupla

Um arranjo semelhante pode ser feito para se observar a difração de fenda dupla. O efeito de difração observado quando a luz passa por cada uma das fendas é o mesmo discutido anteriormente, mas o resultado final em qualquer direção depende da diferença de caminho entre as duas contribuições

Fig. 14.2 – Difração de fenda dupla.

A fig. 14.2 nos mostra que a luz difratada pelas duas fendas sofre efeito de interferência, de modo a se obter no anteparo máximos e mínimos de luz.

A intensidade total é o produto de um fator devido à difração de fenda simples(sinb/b) vezes um fator devido à interferência de fenda dupla (cos (γ)).   O fator de interferência tem um máximo (chamados de máximos principais) sempre que:

 onde m=0,1,2,3,4, ...denota a ordem do padrão.

Já o fator de difração tem mínimos de intensidade sempre que:

 onde n=1,2,3,4, ... denota a ordem do mínimo.

O padrão pode ser descrito dizendo-se que o fator de difração “modula” as variações do fator de interferência. Sempre que um máximo de interferência coincide espacialmente com um mínimo de difração, esse máximo de interferência é suprimido. Assim, sempre que, um máximo do padrão de interferência será eliminado

 

c) Difração de fenda múltipla

.

Fig. 14.3 – Difração de N fendas de largura b período d  a linha serrilhada representa a função de difração  (sinb/b)2 Utilizando a relação apresentada no parágrafo anterior para o caso da fenda dupla, e a relação trigonométrica,  o padrão de  intensidades para a fenda dupla pode ser escrito como:

  A generalização desta expressão ao casso de Nfendas não é uma tarefa matemática simples. O resultado final, contudo, é bastante simples sendo obtido apenas  substituindo-se  por . Assim para a difração por um arranjo de múltiplas fendas, a distribuição de intensidades é dada por:

2 – OBJETIVOS :

– Observar os efeitos de difração de Fraunhofer produzidos por uma fenda e os efeitos de interferência produzidos por duas ou mais fendas.

– Elaborar um modelo que explique as principais características do padrão de interferência e/ou difração observado.

Verificar quantitativamente as previsões do modelo.

3 – PREPARAÇÃO

a – Estude ou revise os conceitos de interferência e difração, principalmente os seguintes pontos:

a.1 – Experimento de Young.

a.2 – Difração.

a.3 – Difração de Fraunhofer de uma fenda.

a.4 – Difração e interferência por fendas múltiplas – rede de difração

b – para explicar quantitativamente o padrão de difração de uma fenda de abertura b, observado em um anteparo a uma distância z, produzida por ondas incidentes planas, de comprimento de onda l e irradiância I₀ .

b.1 – Mostre que a condição para que o padrão de difração possa ser considerado como de Fraunhofer é :

(1)

b.2 – Mostre que nesta condição o padrão de difração pode ser descrito em termos de irradiância como:

(2)onde I₀ é a irradiância em y = 0 e (3)

com k=2p /l e tan q = y/z. Note que para y = 0 este modelo prevê o máximo absoluto (ou máximo central) da irradiância.

b.3 – Se b é 1mm e l = 633 nm, à partir de qual distância z você espera que a eq. (2) seja válida ?

b.4 – Baseado neste modelo, onde você espera achar os primeiros 4 mínimos de difração?

b.5 – Utilizando algum software de sua preferência simule o experimento obtendo um gráfico de I/ I₀ versus y para l = 633nm, b = 0.2mm e z = 3m.

Quanto é aproximadamente a intensidade relativa dos primeiros 10 máximos ?

 

c – Estude o modelo para a interferência de duas fendas com largura b e distância entre fendas h (Experimento de Young) levando em consideração os efeitos de difração.

c.1 – Mostre que se a condição de difração de Fraunhofer for satisfeita, a incidência pode ser escrita como:

.

(4)onde .

c.2 – Simule no computador o padrão para l = 633 nm, b = 0.2 mm, z = 3 m e h = 0.5 mm. Determine a posição dos máximos e mínimos de interferência e de difração.

.

d – Generalize o modelo para o caso de N fendas.

d.1 – Mostre que :

(5).

Verifique que a eq.(5) coincide com a eq. (4) para N = 2.

d.2 – Simule no computador o padrão previsto para N = 3, 4, 5, 10.

Que acontece com a largura dos máximos de interferência, à medida que aumenta N ?

Quantos mínimos de interferência ha dentro do máximo central de difração ( i. é, –p < b < p ) ?

.

4 – PROCEDIMENTO EXPERIMENTAL (veja o resumo das atividades para este semestre)

Os experimentos serão realizados com um Laser de l  desconhecido (cuidado, no laboratório tem laser vermelho, laranja, azul e verde). As fendas foram feitas em um filme de cromo sobre vidro. A largura das fendas b e a separação entre elas d são desconhecidos, mas da ordem de: b @ 30 – 60 m m e d@ 60 – 120 m m

Alinhamento Para que as medidas sejam feitas com precisão, é fundamental que a máscara com as fendas seja colocada perpendicular ao feixe do Laser, isso pode ser facilmente feito enviando o feixe do Laser refletido na superfície do slide, novamente para a saída do Laser.

Medida do espectro angular de espalhamento para 3 situações:

 

Fenda única, fio de cabelo, e rede de difração.

 

 

Medir o espectro ângular, significa medir a intensidade da luz em função do ângulo de observação.

Para esta medida o detector se movimentará linearmente sobre um trilho graduado e perpendicular à direção da incidência

do feixe laser. A medida do ângulo ( na posição dos máximos ou mínimos) correspondente à cada posição do fotodetector no trilho, pode ser feita por triangulação ( Distancia Z conhecida).

Usando o microscópio, medir a largura da fenda , a espessura do fio de cabelo , o período e a largura das fendas da rede de difração. Com as informações das 3 situações diferentes ( fenda única, fio de cabelo e grade de difração) determinar o comprimento de onda do laser utilizado.

Roteiro sugerido:

1 – Montar o conjunto Laser, fenda e detetor no trilho. Projete o padrão de difração/interferência sobre o detetor e registre as intensidades ( Trabalhar sempre na região de linearidade do detector, para evitar que a curva fique achatada pela saturação) e distâncias do máximo central.

2 – Caracterize os padrões de difração/interferência para: 1 fenda, 1 fio de cabelo e N fendas ( N é desconhecido), ou seja, meça as posições dos máximos ou mínimos.

 

3 – No caso de 1 fenda, caracterize os padrões de difração obtidos para várias distâncias fenda-anteparo (z) e verifique se a eq. 2 é válida.

4 – Meça diretamente com o microscópio, as dimensões b e d.

5 –  À partir dos seus dados experimentais, traçar a curva de intensidade difratada para cada uma das 3 situações em função do ângulo de observação.

7– Pode-se concluir que a difração/interferência é um método preciso para medir  l? Qual é a precisão do método?

Obs. O prof. definirá os ítens a fazer

.

5 – BIBLIOGRAFIA

1 – G. R. Fowles, “Introduction to Modern Optics“, Holt, Rinehart and Winston, second edition, New York (1975).

2* – John P. McKelvey and H. Grotch, “Fisica 4 “, Harbra – Harper & Row do Brasil, São Paulo, cap26 (1981).

3 – Francis A. Jenkins and Harvey White,” Fundamental of Optics“, MacGraw Hill. (1976).

4 – Hecht, Eugene, “Optics“. Adelphi University, Addison-Wesley Publishing Company (1990)

.

.

Fig. 14.4 – Figuras de difração produzidas por diferentes números de fendas     d = 3b and N = 1 (superior), N = 2 (centro), and N = 10 (Inferior).

Z (eixo de intensidade) = log[G(y)I(x)/I0 + 10-5] + 5, onde G(y) é a função gaussiana que determina o contorno do feixe laser.

A escala log de intensidade simula a resposta do ôlho para luz intensa. (Simulações: Paulo Dainese e Hugo Fragnito, Nov. 2004).

.

6 – APÊNDICE :

.

a) – DIFRAÇÃO DE UM FIO DE CABELO

Se no lugar de uma fenda simples, colocarmos um fio de cabelo, o padrão de difração produzido por um feixe laser, é muito similar ao da fenda, exceto na pequena região dentro do feixe.

Isto pode ser explicado a partir do principio de Babinet de máscaras complementares. Consideremos duas máscaras complementares como as da figura 14.5, iluminadas em idênticas condições por um feixe de luz.

Sejam E_A e E_B os campos de difração no ponto P produzidos em cada caso:

onde indica a integral de Huygens.Fig. 14.5 – A e B Máscaras complementares.

(ou, mais corretamente, a integral de Kirchoff – Fresnel, mas que de todos modos não é necessário especificar a forma desta integral) f(E) é uma função do campo E na superfície da máscara e ds o elemento de área.

A soma das áreas das duas máscaras (A + B) é a superfície sem obstáculos, onde E(P) é o campo produzido na ausência de máximos.

.Portanto, E_A+ E_B = E

Este resultado é o princípio de Babinet. Este princípio é útil principalmente nos pontos onde E(P) = 0, em cujo caso temos E_A = -E_B e portanto, a irradiância I_A = I_B .

No caso do fio de cabelo iluminado por um feixe Laser, o padrão coincide com o da fenda em todos os pontos, exceto na região dentro do feixe (onde E ¹ 0).

.

b) – REGISTRO FOTOGRÁFICO

Também é possível registrar as figuras através do processo fotográfico, colocando-se um papel fotográfico para ser exposto durante um tempo bem controlado, à luz emitida e difratada pelas fendas.

É preciso mencionar que neste caso, a distância papel-fenda deverá ser bem menor uma vez que as dimensões do papel fotográfico são menores, consequentemente a imprecisão nas medidas a serem feitas nas fotos aumenta, aumentando assim o erro das medidas das fendas.

Lembrar também que a distribuição de luz, ao longo da figura de difração não é homogênea,

resultando em uma imagem com muito contraste no centro e quase nada nas laterais. Essa limitação pode ser superada bloqueando a parte central da imagem, expondo mais tempo as regiões laterais da figura.

.

c ) – PARAFUSO MICROMÉTRICO DO MICROSCÓPIO

.

Fig. 14.6 – Escala do microscópio.

A figura 14.6 mostra a escala do parafuso micrométrico do microscópio usado para se medir as fendas.

O parafuso é composto de 3 escalas:

a) Tambor fixo

i – escala vertical em mm

ii – escala horizontal em 0.001mm

b) Tambor móvel

iii – em 0.01mm ( 1mm dividido em 100 partes)

A cada volta completa do parafuso, a mesa se desloca 1,000 mm( Para maiores detalhes veja as fotos que estão no laboratório).

d) DIFRAÇÃO DE UMA FENDA

.

Fig. 14.7a – Figura de difração de uma fenda.Fig. 14.7b – Figura de difração de uma fenda retangular.

e) DISTRIBUIÇÃO DA INTENSIDADE LUMINOSA

.

Fig.14.8 – Figura da distribuição da intensidade luminosa..Fig.14.9 – Microscópio Metrológico e seus comandos. +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++