Speciation:
In sexually reproducing organisms the genetic changes fixed by natural selection or drift spread quickly through the population, hindering the possibility of its branching into two or more different species. Speciation is commonly associated with geographic isolation, which prevents gene flow between populations and allows each group to follow a different evolutionary path. This is not, however, the only possible mechanism of speciation. In this work we argue that even in a totally homogeneous environment, without geographic barriers, spatially distributed populations can develop inhomogeneity through symmetry breaking and spontaneous pattern formation. Typically, the existence of local but spatially overlapping mating neighborhoods in two-dimensional space may result in a dynamic pattern of polymorphism.
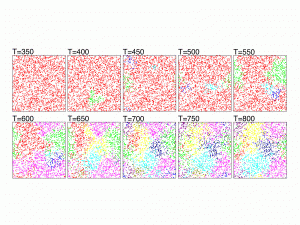
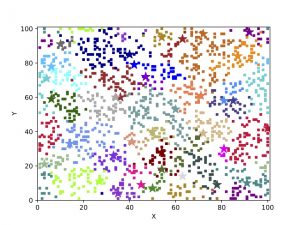
The figure shows the evolution of 2000 genetically identical individuals scattered on a grid of size 128 x 128. The genomes are represented by binary strings of size 125 and mating is allowed only between individuals that differ in no more than 20 genes and are not farther than 5 grid units from each other. The mutation rate per gene is 0.001 and time is measured in generations. Colors represent groups that are reproductively isolated from other groups of different colors, i.e., the genetic distance between any pair of individuals of different colors is larger than 20.
The historical information of the evolution, including all speciation and extinction events that ever occurred, can be stored and used to construct phylogenetic and genealogical trees. We have proposed two algorithms to do that.
The first algorithm focuses on genealogies and the quantity saved is the parenthood of each individual. With parenthood registered, the time to the most recent common ancestor, i.e., the number of generations needed to go backward to find a common ancestor of one individual with another individual of the population, can be easily calculated in terms of the common ancestor of the parents. These times are computed at every generation between all pairs of individuals and, at the end of the simulation, they are saved in a matrix (the Most Recent Common Ancestor Time matrix — MRCAT).
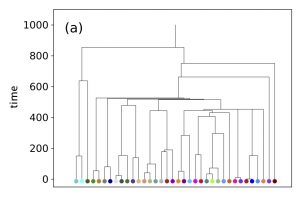
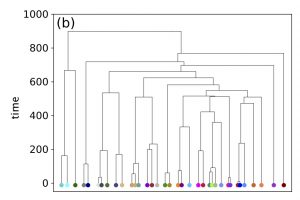
The second algorithm focuses directly on phylogenies and consists in recording all speciation and extinction events (the Sequential Speciation and Extinction Events — SSEE) and set a matrix analogous to MRCAT but whose entries are species rather than individuals. The SSEE matrix contains the exact branching times in the simulated clade or community, including all extinct species.
The SSEE and MRCAT matrices can be used to draw the exact branching sequence of the simulated individuals and species, respectively. The figures shown an example: the final population and the phylogeny of the extant species obtained with SSE and MRCAT.
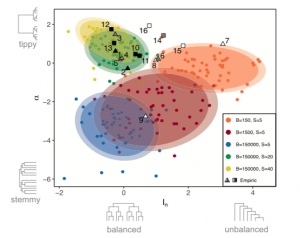
Phylogenetic trees contain signatures of the processes responsible for the speciation events they display. Inferring processes from tree properties, however, is challenging. We used our speciation model to address this problem. We simulated parapatric and sympatric (narrow and wide mating range, respectively) radiations and constructed their phylogenetic trees, computing structural properties such as tree balance and speed of diversification. We showed that parapatric and sympatric speciation are well separated by these structural tree properties. Balanced trees with constant rates of diversification only originate in sympatry and genome size affected both the balance and the speed of diversification of the simulated trees. Comparison with empirical data showed that most of the evolutionary radiations considered to have developed in parapatry or sympatry are in good agreement with model predictions. This is illustrated in the figure below,
Global patterns of speciation and diversity
M. A. M. de Aguiar, M. Baranger, E. M. Baptestini, L. Kaufman and Y. Bar-Yam. Nature 460 (2009) 384
Error catastrophe in populations under similarity-essential recombination
M. A.M. de Aguiar, D. M. Schneider, E. do Carmo, P. R. A. Campos, A. B. Martins, J. Theor. Biol. 374 (2015) 48-53.
The mutation-drift balance in spatially structured populations
D. M. Schneider, M. A.M. de Aguiar, A. B. Martins, J. Theor. Biol. 402 (2016) 9-17.
Registering the evolutionary history in individual-based models of speciation Carolina L. N. Costa, Flavia M. D. Marquitti, S. Ivan Perez, David M. Schneider, Marlon F. Ramos, Marcus A.M. de Aguiar, Physica A 510 (2018) 1-14.
Signatures of microevolutionary processes in phylogenetic patterns Carolina L. N. Costa, Paula Lemos-Costa, Flavia M. D. Marquitti, Lucas D. Fernandes. Marlon F. Ramos, David M. Schneider, Ayana B. Martins, Marcus A.M. de Aguiar, Systematic Biology 68 (2019) 131
Population dynamics: voter and Moran models
The voter model simulates the dynamics of an election between two candidates in an election. The voters’ opinions can be influenced by their friends and also by opinion makers, such as journalists or politicians, whose power of persuasion toward one of the candidates extends over the entire population. The voters are modelled as nodes of a network of contacts and the opinion makers by additional (external) nodes whose states are fixed and that reach all voters equally, acting as a perturbation to the intrinsic dynamics.
The Moran model, on the other hand, describes the evolution of a population of haploid individuals bearing a single gene with two alleles. In the original model the dynamics consists in replacing an individual chosen at random by a copy of another individual, also picked at random. Here we introduce a slightly different version of the dynamics in which an individual is chosen at random and is replaced by its offspring. The offspring is obtained by sexual reproduction between the expiring individual and a mating partner which is also chosen at random among the remaining individuals. The offspring can keep the allele of the expiring individual or that of the mating partner with 50% probability. If the offspring keeps the allele of the expiring individual, the population remains unchanged. If it inharits the allele of the mating partner, the net effect is that the expiring individual is replaced by a copy of the latter. This alternative dynamics is identical to the Moran process except that it runs twice as slow. The advantage is that we can now introduce mutations during the birth process by allowing the allele received from either parent to change. If we further replace the random choice of the mating partner by a neighbour in a network, the Moran model can be mapped exactly into the Voter Model for any regular network, where the number of neighbours of every node is the same. In particular, the map is exact for fully connected networks, which corresponds to the original panmictic model.
We have solved the voter model exactly for fully connected networks here:
Dynamical response of networks under external perturbations: exact results
David D. Chinellato, Irving R. Epstein, Dan Braha, Yaneer Bar-Yam and Marcus A. M. de Aguiar,
J. Stat. Phys. 159(2) (2015) 221-230.
and provided semi-analytic expressions for the star network:
Binary dynamics on star networks under external perturbations
Carolina A. Moreira, David M. Schneider and Marcus A.M. de Aguiar,
Phys. Rev. E 92 (2015) 042812.
The mapping between the Moran and Voter model for regular networks was demonstrated here
The mutation-drift balance in spatially structured populations
David M. Schneider, Marcus A.M. de Aguiar, Ayana B. Martins,
J. Theor. Biol. 402 (2016) 9-17.
and applications of the model can be found below.
Anticipating Economic Market Crises Using Measures of Collective Panic
Harmon D, Lagi M, de Aguiar MAM, Chinellato DD, Braha D, Epstein IR, et al.
PLoS ONE 10(7) (2015) e0131871. doi:10.1371/journal.pone.0131871
Voting contagion: Modeling and analysis of a century of U.S. presidential elections
Dan Braha and Marcus A.M. de Aguiar,
PLoS ONE 12(5): e0177970.
Opinion Dynamics on Networks under Correlated Disordered External Perturbations
Marlon Ramos, Marcus A.M. de Aguiar, Dan Braha.
J. Stat. Phys. 173 (2018) 54-76
Ring Species:
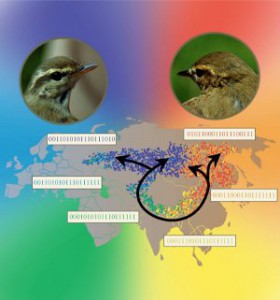
Ring species are rare and fascinating structures. One of the best studied examples occurs with the birds Greenish Warblers around the Tibetan plateau in Asia. Up to about ten thousand years ago their population was restricted to the forests to the south of the plateau. With the end of last glaciation the forest expanded to the north around the plateau, to the east and to the west and the birds followed the expansion. Two thousand years later when the two expanding fronts of the forest met at the north the population of birds also met their old relatives. However, they had evolved so much that they would not recognize each other as belonging to the same species and would not mate. What makes this very special is that, around the ring of populations that formed around the plateau, from the northeast through the south and to the northwest, there no break in the gene flow: it is a single species with a clash at the north.
The figure shows the result of a simulation with colors indicating genetic difference. The only point of incompatibility is between the blues and the reds at the north.
Evolution and Stability of Ring Species
Ayana B. Martins, M.A.M. de Aguiar and Y. Bar-Yam,
PNAS 110(13) (2013) 5080.
Barriers to gene flow and ring species formation
Ayana B. Martins and Marcus A.M. de Aguiar,
Evolution 71(2) (2017) 442-448, doi:10.1111/evo.13121
Book: Tópicos de Mecânica Clássica (in Portuguese)